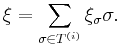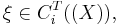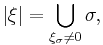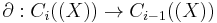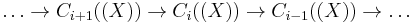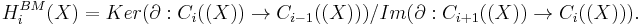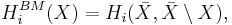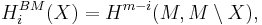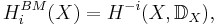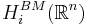Borel–Moore homology
In mathematics, Borel−Moore homology or homology with closed support is a homology theory for locally compact spaces, introduced by Borel and Moore (1960).
For compact spaces, the Borel−Moore homology coincide with the usual singular homology, but for non-compact spaces, it usually gives homology groups with better properties.
Note: There is an equivariant cohomology theory for spaces upon which a group  acts which is also called Borel cohomology and is defined as
acts which is also called Borel cohomology and is defined as 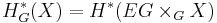 . This is not related to the subject of this article.
. This is not related to the subject of this article.
Contents |
Definition
There are several ways to define Borel−Moore homology. They all coincide for spaces  that are homotopy equivalent to a finite CW complex and admit a closed embedding into a smooth manifold
that are homotopy equivalent to a finite CW complex and admit a closed embedding into a smooth manifold  such that
such that 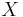 is a retract of an open neighborhood of itself in
is a retract of an open neighborhood of itself in 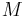 .
.
Definition via locally finite chains
Let 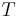 be a triangulation of
be a triangulation of 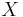 . Denote by
. Denote by 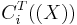 the vector space of formal (infinite) sums
the vector space of formal (infinite) sums
Note that for each element
its support,
is closed. The support is compact if and only if 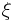 is a finite linear combination of simplices.
is a finite linear combination of simplices.
The space
of i-chains with closed support is defined to be the direct limit of
under refinements of 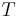 . The boundary map of simplicial homology extends to a boundary map
. The boundary map of simplicial homology extends to a boundary map
and it is easy to see that the sequence
is a chain complex. The Borel−Moore homology of X is defined to be the homology of this chain complex. Concretely,
Definition via compactifications
Let 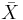 be a compactification of
be a compactification of 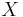 such that the pair
such that the pair
is a CW-pair. For example, one may take the one point compactification of 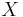 . Then
. Then
where in the right hand side, usual relative homology is meant.
Definition via Poincaré duality
Let 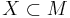 be a closed embedding of
be a closed embedding of 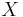 in a smooth manifold of dimension m, such that
in a smooth manifold of dimension m, such that 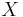 is a retract of an open neighborhood of itself. Then
is a retract of an open neighborhood of itself. Then
where in the right hand side, usual relative cohomology is meant.
Definition via the dualizing complex
Let
be the dualizing complex of 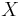 . Then
. Then
where in the right hand side, hypercohomology is meant.
Properties
- Borel−Moore homology is not homotopy invariant. For example,
vanishes for 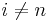 and equals
and equals 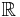 for
for 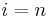 .
.
- Borel−Moore homology is a covariant functor with respect to proper maps. Suppose
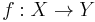 is a proper map. Then
is a proper map. Then 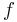 induces a continuous map
induces a continuous map 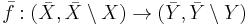 where
where 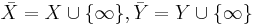 are the one point compactifications. Using the definition of Borel−Moore homology via compactification, there is a map
are the one point compactifications. Using the definition of Borel−Moore homology via compactification, there is a map 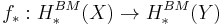 . Properness is essential, as it guarantees that the induced map on compactifications will be continuous. There is no pushforward for a general continuous map of spaces. As a counterexample, one can consider the non-proper inclusion
. Properness is essential, as it guarantees that the induced map on compactifications will be continuous. There is no pushforward for a general continuous map of spaces. As a counterexample, one can consider the non-proper inclusion 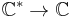 .
.
- If
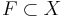 is a closed set and
is a closed set and 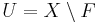 is its complement, then there is a long exact sequence
is its complement, then there is a long exact sequence
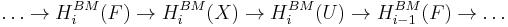 .
.
- One of the main reasons to use Borel−Moore homology is that for every orientable manifold (in particular, for every smooth complex variety)
 , there is a fundamental class
, there is a fundamental class ![\ [M]\in H^{BM}_{top}(M)](/2012-wikipedia_en_all_nopic_01_2012/I/145fe878d7f376bf61bce473a992bb5d.png) . This is just the sum over all top dimensional simplices in a specific triangulation. In fact, in Borel−Moore homology, one can define a fundamental class for arbitrary (i.e. possibly singular) complex varieties. In this case the set of smooth points
. This is just the sum over all top dimensional simplices in a specific triangulation. In fact, in Borel−Moore homology, one can define a fundamental class for arbitrary (i.e. possibly singular) complex varieties. In this case the set of smooth points 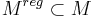 has complement of (real) codimension 2 and by the long exact sequence above the top dimensional homologies of
has complement of (real) codimension 2 and by the long exact sequence above the top dimensional homologies of 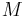 and
and 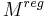 are canonically isomorphic. One then defines the fundamental class of
are canonically isomorphic. One then defines the fundamental class of 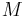 to be the fundamental class of
to be the fundamental class of 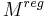 .
.
References
- Iversen, Birger Cohomology of sheaves. Universitext. Springer-Verlag, Berlin, 1986. xii+464 pp. ISBN 3-540-16389-1 MR0842190
- Borel, Armand; Moore, John C. (1960), "Homology theory for locally compact spaces", The Michigan Mathematical Journal 7: 137–159, ISSN 0026-2285, MR0131271, http://projecteuclid.org/euclid.mmj/1028998385